Content
In this lecture we will study semi-Riemannian manifolds, mainly concentrating on Lorentzian manifolds, assuming basic knowledge about Riemannian manifolds as provided e.g. in the lecture "Differential geometry I" by Clara Löh.Lorentzian manifolds arise when one combines n-dimensional space and time to an (n+1)-dimensional manifold. An understanding of Lorentzian manifold is the key ingredient to understand the theoretical aspects of general relativity.
A Lorentzian metric is a symmetric (0,2)-tensor g on a manifold of dimension n+1, such that in every p∈M there is a basis (e0,...,en) with g(eij)=0 for i ≠ j, g(e0,e0)=-1, and g(ei,ei)=1 for i>0. In other words, up to the minus sign, the definition coincides with the one of a Riemannian manifold.
Many aspects that you know from Riemannian geometry also hold for Lorentzian manifolds, we just have to add some signs at some places. These manifolds may be curved, and important notions of curvature are sectional curvature, Ricci curvature and scalar curvature. The famous Einstein equations are a statement about the Ricci curvature of the Lorentzian manifold describing our universe, e.g. vacuum spacetime is simply a Lorentzian manifold with vanishing Ricci curvature.
This allows to study important examples, as e.g. the Schwarzschild solution which is a (3+1)-dimensional manifold with vanishing Ricci-curvature, but non-zero sectional curvature.
Other examples are so-called Robertson-Walker spacetimes which are used to model the evolution of the universe.

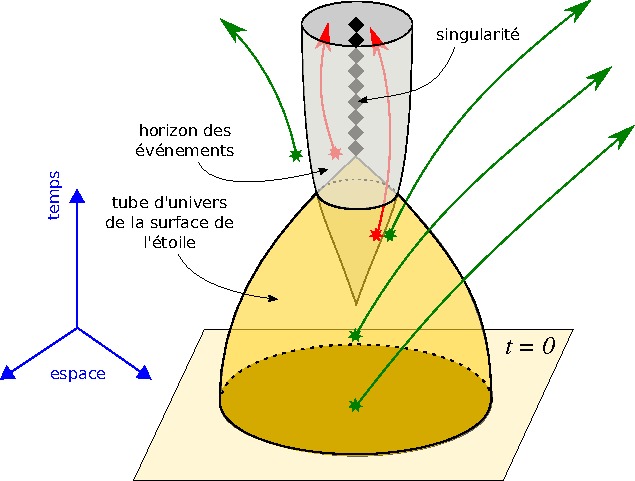
This picture arose from computer calculations using basic properties
of Lorentzian manifolds. It represents a black hole.
The image was obtained from the web page linked here
Picture created by Alain Riazuelo, IAP/UPMC/CNRS under the license CC-BY-SA 3.0.